Final Study Notes

Karatsuba Algorithm

• Used to multiply two integers $x, y$
• The idea is to break the multiplication problem into three smaller problems

$xy=z_0\cdot 2^{2m}+z_1 \cdot 2^m+z_2$
$z_0=x_1y_1$
$z_1=(x_1z_2+x_2z_1)$
$z_2=x_2y_2$

• Note that there are 4 multiplications, which yields the following recurrence

$T(n)=4T(\frac{n}{2})+O(n)$

• By Master's Theorem, this still yields a runtime of $O(n^2)$
• Consider the following property

$(x_1+x_2)(y_1+y_2)=x_1 y_1+(x_2y_2+x_2y_1)+x_2y_2$
$(x_1+x_2)(y_1+y_2) - x_1 y_1-x_2y_2 = (x_2y_2+x_2y_1)$
$z_1=(x_1+x_2)(y_1+y_2) - x_1 y_1-x_2y_2$

• Substitute back to the original equation, we can see that we have reduced the problem into 3 multiplication problems

Strassen Algorithm

$C=A\times B$

• All the matrices are $n\times n$
• Matrix multiplication by breaking the matrices ($A, B$ and $C$) into the four quadrants and calculate the quadrants separately
• Strassen came up with 7 additonal matrices $M_1\cdots M_7$ that can be generated from the quadrants of $A$ and $B$ which can be used to calculate the quadrants of $C$
• Since each recursion is calculating 7 matrices of $n/2$ by $n/2$ size, the recurrence is $T(n)=7T(n/2)+O(n)$
• See notes on Lecture 04 for more details

Saddleback Search

• Finding an element in a matrix with sorted rows and columns

Steps

1. Start from the top right elements
2. If the element is smaller than the desired number move down
3. If the element is greater than the desired number move left

i = 0
j = n
while i <= n and j >= 0 do
    if M[i, j] = x
        return (i, j)
    else if M[i, j] < x
        i = i + 1
    else
        j = j - 1

return "not found"

• Runtime complexity of $O(m+n)$ where $m$ and $n$ is the dimension of the matrix

Matrix Searching with Divide and Conquer

1. Binary search on row $m/2$
2. If $x$ is found return
3. Otherwise, find $M[m/2, n_1] < x$ and $M[m/2, n_1 + 1] > x$
4. $n_2=n-n_1$

Time complexity: $T(m, n)=T(m/2, n_1)+T(m/2, n_2) + \log n$

2D Maxima

• Assume no two points have the same x-axis

• Sort the points according to x-axis

• If $n<5$ solve the problem by definition and return the maxima

• Partition the points into $n/2$ size partitions and solve the two partitions recursively

• Compute the largest y-axis in the last $n/2$, let it be $m_y$

• The solution is combining the solution from the second solution and all points that has a y-axis greater than $m_y$ in the first partition

Weighted Total Completion Time

• Sort all jobs according to process time per unit weight

Fractional Knapsack

• Each item has a weight $w_i$, and a per unit weight value $v_i$
• There is a total capacity $W$ which denotes the total amount of weight that the knapscak can hold

• The idea is maximize the value in the knapsack while not exceeding the total weight

• Sort the items according to per unit weight value (descending order)

• Iterate through all the elements

• If there are remaining weights for the item add as much to the knapsack as possible

• Do nothing if the current remaining weight is less than the unit weight of the item

Gale Shapely Algorithm

• To solve the stable matching algorithm
• Consider the student/manager matching problem

while there is an unpaired manager M
    Let M propose to his favourite student whom he never tried before
    If student is not paired
        Pair
    Else if student prefers the new manager over his old manager
        Pair the student with new manager, and turn old manager unpaired

• Time complexity is $O(n^2)$
• A student's manager only gets better during the pairing process
• A manager always tries from his most favourite to his least favourite student in order
• Can prove correctness by contradiction
  • Assume there is an unstable pair
  • Manager should have never propsed to student since the student's manager only gets better
  • If manager favours the student in question more than his favourite student he should have proposed to him before, contradiction

Linear Independent Set

• A list of items 1...n each with a weight
• A linear independent set is a set of items which doesn't contain adjacent items from the list
• The goal is to find such a set and maximize weight

Solution

• The idea is to create a one dimensional DP table where DP[k] is the optimal solution using the first $k$ items

• There can be only two cases, either $k$ is in the set or it is not

If it's not in the set

$D[k]=D[k-1]$

• This essentially means that the optimal solution is the same solution as the solution for $k-1$ since $k$ has no effect on the optimal solution

If it's in the set

$D[k]=D[k-2]+w_k$

• Since $k$ is part of the solution $k-1$ cannot be part of the solution by definition, so we take the $k-2$ case and add the weight of $k$

• Since our goal is to maximize the total weight, we take the max of the two cases to get the reccurrence

$D[k]=\max\{D[k-1],D[k-2]+w_k\}$

• The runtime is $O(n)$
• See Lecture 10 for pseudocode

Fun Fact: The name "Dynamic Programming" was invented in 1952 by Richard Bellman

Weighted Interval Scheduling

• Each job has a price
• Maximize the revenue instead of number of jobs served

Solution

• Let $D[k]$ be the value of the optimal solution for the first $k$ intervals
• Define the function $l(t)$ to return the last interval that finish earlier than time $t$
• There are two cases, at optimal solution for $k$, $k$ can either be in the solution or not

If it's in the solution

• Let $s_k$ be the starting time of interval $k$

$D[k]=D[l(s_k)]+w_k$

• If it is in the solution, find the optimal solution for the latest interval that does not conflict with the current interval

If it's not in the solution

$D[k]=D[k-1]$

• Self explanatory

• To maximize the two cases

$D[k]=\max\{D[k-1],D[l(s_k)]+w_k\}$

Longest Common Subsequence

• For example war is a subsequence of waterloo
• The goal is to find the longest common subsequence given two strings $S$ and $T$
• Create a DP table that represents the length of the LCS for $S[1\cdots i]$ and $T[1\cdots j]$
• There are three cases, either $T[j]$ appears in the LCS, $S[j]$ appears in the subsequence or both appears in the LCS

S[i] not in the LCS

$D[i,j]=D[i-1,j]$

• Since $S[i]$ is not in the sequence, it is the same as the optimal solution as $S[i-1]$

T[j] not in LCS

$D[i, j]=D[i, j-1]$

• Self explanatory

Both in the LCS

$D[i, j]=D[i-1, j-1]+1$

• Since they are equal to each other, add one to the LCS

• Since the goal is to maximize the length, we maximize the three cases by

$D[i, j]=\max\{D[i-1,j],D[i,j-1],D[i-1,j-1]+\delta(s[i],T[j])\}$

where $\delta(a,b)=1$ if $a=b$, 0 otherwise

• Need a backtracking algorithm after constructing the DP table

Edit Distance

• The minimum amount of edits needed to transform $S$ to $T$
• Operations include deletion, insertion, substitution of a letter
• Three cases are S[j] is deleted, T[j] is inserted, and nothing happens

• Very similar to LCS, when an operation is performed (Case 1 and Case 2), add 1 to the latest entry to the DP table, else do nothing (Case 3)

• Take the min instead of max

$D[i,j]=\min\begin{cases} D[i-1,j]+1\\ D[i,j-1]+1\\ D[i-1,j-1]+\delta(S[i],T[j]) \end{cases}$

Where $\delta(S[i],T[j])=0$ if $S[i]=T[j]$, 1 otherwise

Longest Increase Subsequence

• Create a one dimensional DP table with where $D[k]$ represents the optimal length of the subsequence up to the $k$th number

$D[i]=1+\max_{j < i~{} and ~{} a_j < a_i}D[j]$

• Basically means find the solution with the greatest value that comes before $j$ and has

Maximum Subarray

• Given array $A$

$D[i]=\max\{0, D[i-1]+A[i]\}$

Non-canonical Change Making

• The idea is to create a DP table, where $D[k]$ epresents the minimum coin needed to make up value $k$
• Find the optimal solution of which coin that you insert last will give you the optimal solution

$D[n]=1+\min_{i=1\cdots k} D[n-d_i]$

Subset Sum

• Whether the sum $K$ is able to be constructed from array $A$
• The DP table $D[i, k]$ stores whether a solution is possible with the first $i$ entries in the array and the given number $k$

$D[i,k]=D[i-1, k-a_i]~{} or ~{} D[i-1,k]$

• The two parts in the recurrence denotes the two cases, either $a_i$ is used or $a_i$ is not used in the construction, we'll take any one that yields a solution

Graph Definitions

Acyclic Graph - a graph without cycles
Minimum Spanning Tree - a spanning tree is a spanning tree of a weighted graph with the minimum possible weight

Arc - another name for a directed edge

Strongly connected - a directed graph is strongly connected if every pair of vertices are reachable from each other

Directed acyclic graph (DAG) - a directed graph without any directed cycles

Prim's Algorithm

• A greedy algorithm that finds the MST in a undirected graph

• Choose an arbitrary vertex from the graph and add to the MST

• Grow the MST by adding the minimum weighted edge that has only one vertex in the current MST

• Repeat step 2 until all the vertices in the graph are covered

// vertex set
C = {s}
// edge set
T = {}
while C != V do
    find the edge e = (u, v) with the min weight with u in C and v not in C
    C.add{v}
    T.add{e}

return T

Time Complexity: $O(m\log m)$

$O(m + n\log n)$ using a Fibonacci heap

Kruskal's Algorithm

• Another greedy algorithm that finds the MST

• Sort the edges according to weights

• Iterate through the edges, if the MST $T$ remains acyclic when $e$ is added to $T$, add $e$ to $T$

• Stop when it finishes all the edges

• Can check cycles by assigning a unique set ID for each vertices and check if the vertices are in the same set by comparing the ID (same ID indicates a cycle)

• Can use an array that stores the ID for any given vertex, rename the ID in the smaller set during union

BFS Tree Properties

• A BFS tree has layers
• Layer number of $v$ equals to the shortest distance from $s$ to $v$
• All edges are within the same layer or between two adjacent layers

Directed Graph

• The third property no longer holds
  • There may be edges connecting two vertices with layer number differ by 2 or more (but these edges can only go "backward")

DFS Tree Properties

• u is an ancestor of v if u is on the path from v to the root of the tree
• A back edge is an edge that's not on the DFS tree (but on the original graph) such that one vertex is another's ancestor
  • All non-tree edges are back edges
• Each edge connect a pair of ancestor and descendant

Start/Finishing Times

• For every two vertices $u, v$, the intervals [start(u), finish(u)] and [start(v), finish(v)] are either disjoint or one is contained in another
  • In the second case, u, v are an ancestor-descendent pair

Directed Graph

• The third property no longer holds

Strong Connectivity

1. Pick an arbitrary edge on the graph
2. Use DFS to check if every vertex is reachable from $s$
3. Reverse all the edges
4. Perform step 2 again
5. Return "yes" if both checks returns "yes"

Time complexity: $O(n+m)$

Topological Ordering

1. Find a vertex with inDegree of 0 and make it the first vertex in the ordering
2. Remove the vertex from the graph
3. Find a vertex with inDegree of 0 and assign it $i+1$ in the ordering
4. Repeat 2-3 until the graph is empty

Time complexity: $O(m+n)$

Alternative Method

• For every arc (u, v), finish[v] < finish[u]

• Run DFS on the whole graph, and record the vertices with decreasing finished time during DFS

• Check if the ordering is a topological ordering. Output the ordering if "yes", otherwise output "cyclic"

Strongly Connected Components

Reverse edge direction of G to get G'
DFS on G' to obtain finish time for each vertex
while G is not empty
    find v in G such that v has the latest finishing time
    Do DFS(v) on G to find a strongly connected component C
    Output C
    G = G - C

Time complexity: $O(n+m)$

Dijkstra's Algorithm

• Find the shortest path (in terms of weight) in a positively weighted graph

• Create an unvisited set with all nodes

• Assign to every nodes a tentative distance value, initialize everything to infinity except for the initial node which is set to 0

• Select an unvisited node with the minimum tentative distance and set it as visited

• For all neighbours of the node, set the tentative distance to $d(current)+w(current,neighbour)$ if the assigned weight of that neighbour is greater than the new weight

• Go back to step 3 unless the destination node is visited (finished) or the selected min node has a tentative distance of infinity (no path to the destination)

TIme complexity: $O((n+m)\log n)$ or $O(n\log n + m)$ using a Fibonacci Heap

Bellman-Ford Algorithm

• Find the shortest path with possible negative edges but no negative cycle using DP
• Note that with no negative cycles, the shortest path has at most $n-1$ edges

$D[v, k]=\min_{u: (u, v)\in E)}(D[u, k-1]+w(u, v))$

• Where $D[v, k]$ denotes the shortest distance from $s$ to $v$ given the maximum allowable edge count of $k$

d[s] = 0
d[v] = infinity for all v != s
p: table that denotes the preceding vertex of a vertex for backtracking
for k from 1 to n-1 do
    for each edge (u, v) in E do
        if d[u] + w(u, v) < d[v] do
            d[v] = d[u] + w(u, v)
            p[v] = u

d[desination] is the shortest distance            
backtrack using p

Time complexity: $O(mn)$

Floyd-Warshall Algorithm

• Find the shortest distance for every pair of vertices in a directed graph

Let $D[u, v, k]$ be the shortest distance between u and v using vertices $v_1, v_2, \cdots, v_k$ in between, assume $D[u, v, k-1]$ is computed

Case 1: $v_k$ is not on the shortest path, $D[u, v, k]=D[u, v, k-1]$

Case 2: $v_k$ is on the shortest path, then $D[u, v, k]=D[u, v_k, k-1] + D[v_k, v, k-1]$, since they both use the path $v_1, v_2, \cdots v_k$

Combining the two cases:

$D[u, v, k]=\min\begin{cases} D[u, v, k-1]\\ D[u, v_k, k-1]+D[v_k, v, k-1]\end{cases}$

D[u, v, 0] = infinity for all (u, v) that's not in the edge set
D[u, v, 0] = w(u, v) for all edges (u, v) within the edge set

for k from 1 to n do
    for all u in V do
        for all v in V do
            vk = k th vertex
            D[u, v, k] = min(D[u, v, k-1], D[u, vk, k-1] + D[V[k], v, vk])

Time complexity: $O(n^3)$

Polynomial Reduction Problem Terminologies

Clique - a subgraph in which there exists an edge between every pair of vertices
Independent set - a set of vertices in the graph in which none of two are adjacent
Vertex cover - a set of vertices in which every edge in the graph is incident to at least one vertex in the set

Hamiltonian Cycle - a cycle that visits each vertex exactly once

Hamiltonian Path - a path that visits each vertex exactly once

NP - if the output can be verified by the verifier in polynomial time

Set cover - given a collection of sets $S_i,i=1\cdots m$ in which $S_i \subset S$. Find the minimum collection of set where the union of the sets produces $S$

Set packing - given a collection of sets $S_i, i=1\cdots m$ in which $S_i \subset S$. Find the maximum collection of sets where they don't overlap (i.e. intersecting all of the sets produces an empty set)

Reducing Clique to Independent Set

• Assume $I$ is an instance of a clique
• Reduce it to an instance of an independent set $I'$ by constructing a new graph where an edge exists in the IS instance iff it doesn't exist in the clique instance
• Prove forward "yes" by arguing that since we know every pair of vertices are connected in $I$ then it implies that they are not connected in $I'$, therefore we can say it is an "yes" instance of IS
• Can prove backward "yes" using similar arguments

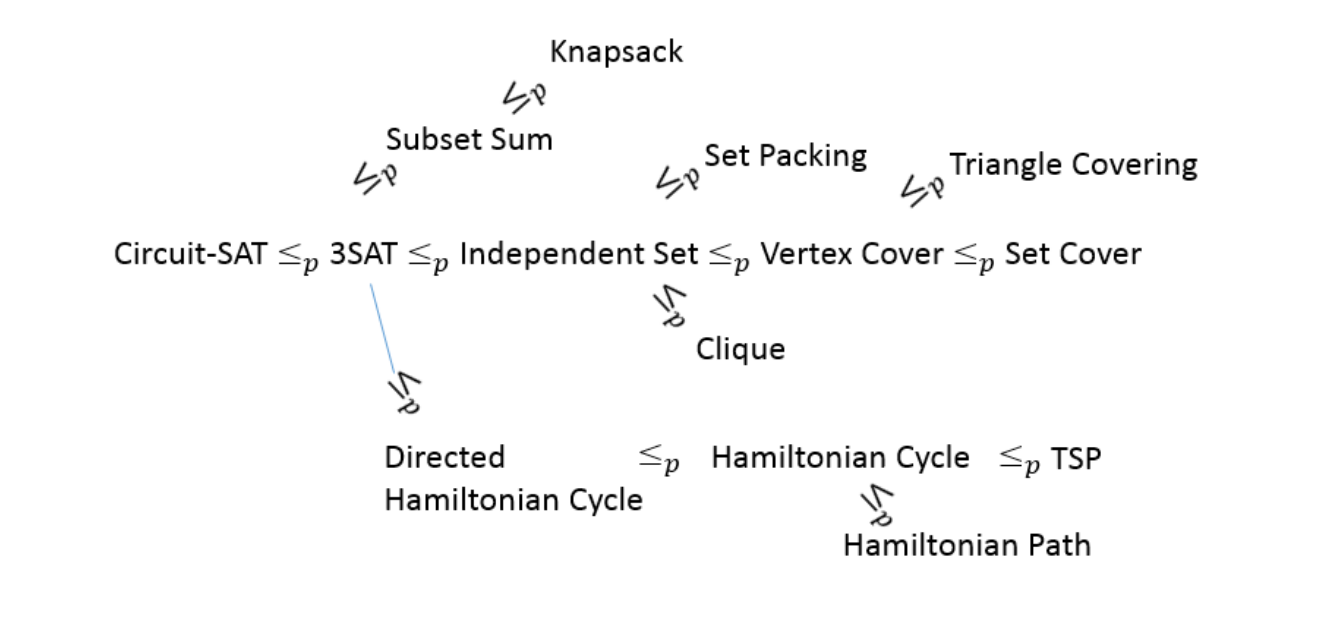
Reduction Tree

Halting Problem

• Assume there is an algorithm that solves the halting problem such that $H(P, I)$ returns yes if $P$ halts given input $I$ and no otherwise (given infinite time)

P(A, I)
    // If A halts on I, loop forever
    if H(A, I) = yes do
        while (true) {}
    // Otherwise halt
    return 1

• Now consider the input $P(P, P)$
• If $P$ halts on $P$, then $H(P, P)$ returns yes and $P$ will loop forever, this is a contradiction
• If $P$ does not halt on $P$, then $H(P, P)$ returns no and $P$ halts, this is a contradiction
• The conclusion is $H$ does not exist and the Halting Problem is undecidable