Logic Coverage

Predicate - an expression that evaluates to a boolean value

Clauses - predicates withtout logical operators

Logic Operators

$\neg$: negation
$\wedge$: and
$\vee$: or
$\rightarrow$: right arrow
$\oplus$: xor
$\leftrightarrow$: equivalence

Notations

$P$: a set of predicates
$C$: all caluses making up the predicates of $P$

$C_p$: caluses of the predicate $p$

Coverages

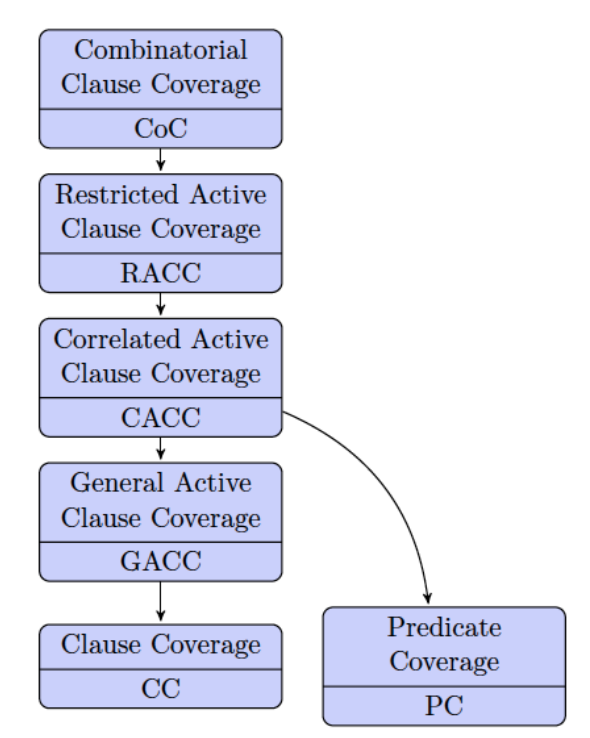
Predicate Coverage (PC)

For each $p\in P$, TR contains two requirements

1. $p$ evaluates to true

2. $p$ evaluates to false

3. Analogous to edge coverage on a CFG

4. Very coarse grained

Caluse Coverage (CC)

For each $c\in C$, TR contains two requirements

1. $c$ evaluates to true
2. $c$ evaluates to false

Combinatorial Coverage (CoC)

For each $p\in P$, TR has test requirements for the clauses in $C_p$

• Also known as multiple condition coverage
• Unscalable, since the number of test requirements while finite, grows exponentially.

Symbol for Clause and Predicate

For predicate $p$ and clause $c$

$p_c=true$: $c$ replaced by true
$p_c=false$: $c$ replaced by false

e.g. $p=a\wedge c$
$p_c=true \Rightarrow a\wedge true$

• If $c$ can never determine $p$, then $c$ is redundant with respect to $p$
  • You can write $p$ without using $c$

Constructing a Truth Table

$p_a=p_{a=true}\oplus p_{a=false}$

If the major clause is $a$, then the row in the truth table is testable for a if $p_a = true$

Active Clause Coverage (ACC)

For each $p\in P$ and making each caluse $c_i\in C_p$ major, choose assignments for minor clauses $c_j$, $j\neq i$ such that $c_i$ determines $p$. TR has requirements for each $c_i$: $c_i$ evaluates to true and $c_i$ evaluates to false.

• The $c_j$s may be different when $c_i$ evaluates to true and $c_i$ evaluates to false.
• No restriction on the $c_j$

General Active Clause Coverage (GACC)

For each $p\in P$ and letting each clause $c_i\in C_p$ be a major caluse, choose minor cluase value $c_j$ such that $c_i$ determines $p$. TR contains two test requirements for each $c_i$: $c_i$ evaluates to true and $c_i$ evaluates to false.

• Does not subsumes $PC$ but subsumes $CC$

Correlated Active Cluase Coverage (CACC)

For each $p\in P$ and letting each clause $c_i$ be major, choose minor clause values for $c_j$ such that $c_i$ determines $p$. TR contains two requirements for each $c_i$: $c_i$ evaluates to true and $c_i$ evaluates to false.

The values chosen for $c_j$ must cause $p$ to be true and for one value of $c_i$ and false for the other.

• Values chosen for $c_j$ must cause $p$ to be true for one value of $c_i$ and false for the other
• Must also satisfy GACC
• Must make $p$ true and false for each clause

Restricted Active Clause Coverage (RACC)

For each $p\in P$ and letting each clause $c_i$ be major, choose minor clause values for $c_j$ such that $c_i$ determines $p$. TR contains two requirements for each $c_i$: $c_i$ evaluates to true and $c_i$ evaluates to false.

The values for each $c_j$ must be the same when $c_i$ is true and when $c_i$ is false

• Must have the same minor caluse in the test set for each major clause
• Harder to satisfy

Infeasibility

• A test requirement $t$ is infeasible if no test case can satisfy test requirement $t$.

Could be caused by

• Predicate is unreachable in its context
• Method containing the predicate never assigns appropriate values to its variables to cause the desired caluse values
• A cluase never determines a predicate and you are trying to achieve an active cluase coverage criterion

Workarounds

1. Satisfy feasible test requirements, dro pinfeasible test requirements
2. If you can't satisfy a particular coverage criterion, use a looser criterion (e.g. settle for CACC if you can't satisfy RACC)

Achieving Logic Coverage

1. Identify the predicates $p\in P$ in the program fragement under test
2. Figure out how to reach each of the predicates
3. Make $c$ determine $p$ (for the active clause criteria$$
4. Find values for variables to meet various criteria