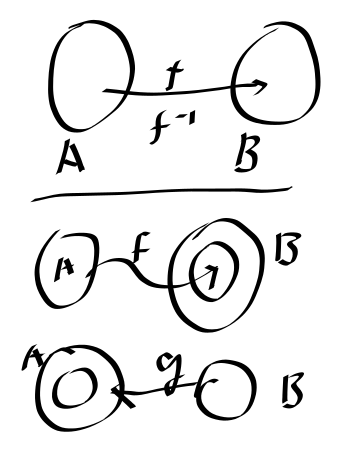Polynomial Time Reduction

• Take any instance $I_a$ in A and map to an instance $I_b$ in B
• f runs in polynomial time
• $I_a$ is yes instance $\Leftrightarrow$ $f(I_a)$

Longest Increasing Subsequence

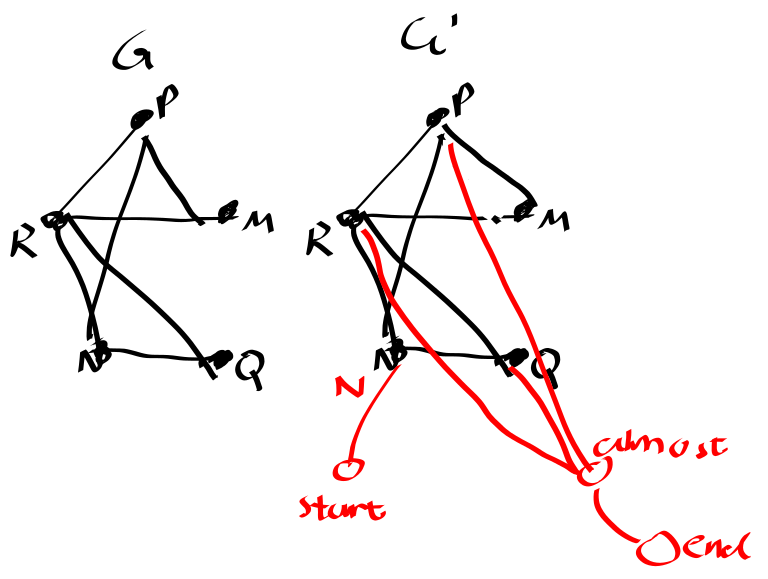
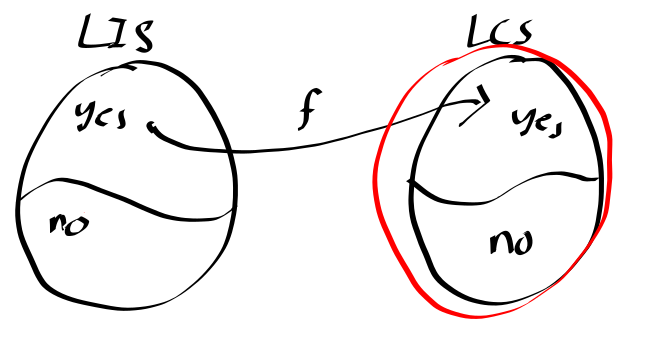
Let the problem in LIS be $A([1, 5, 3, 2], 2)$ yes

Let the problem in LCS be $B([1, 5, 3, 2],[2, 3, 4], 2)$

Let $(L, k)$ be an instance of LIS, construct an isntance of LCS as fllows

Let $L'$ be the sorted list from $L$ in increasing order, then $(L, L', k)$ is an instance of LCS

• Need to prove it runs in polynomial time
• Need to prove that a yes will be mapped to a yes and a no will be mapped to a no

$A\leq_p B$

Thoery: the $\leq_p$ relation is transitive. That is if $A\leq_p B$, $B\leq_p c$, then $A\leq_p C$

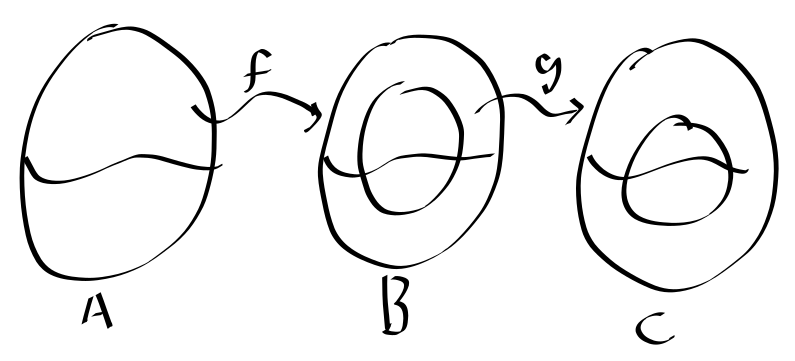
• Proof that this runs in polynomial time

Suppose $f$ runs in $O(n^a)$, $g$ runs in $O(n^b)$

$|I_A|$

$f(I_A)=O(n^a)$

$A\leq_p B, B\leq_p A$

Clique

Consider the following graph

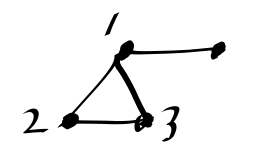
$\{1, 2, 3\}$ is a clique

Independent set $<G, k>$

$\{2, 4\},\{3, 4\}$

Vertex cover $<G, k>$

$\{1, 2\}, \{1, 3\}$

Theory: Clique is $\leq_p$ for independent set

Proof:

Clique instance $I=<G, k>$

Let $\overline{G}$ be the component graph of $G$. Then $I'=<\overline{G}, k>$ is an instance of IS

• Polynomial time $V$
• Yes => Yes. If I has a clique, $V'\leq V$ of size $k$

Then for every $u, v\in V'$, $(u, v)\in E$. Therefore, $(u, v)\notin \overline{E}$. This proves that $V'$ is an IS of size $k$ for $I'$

• $I$ is no => $I'$ is no
• $I'$ is yes => $I$ is yes

Suppose $V'$ is a size $k$ clique for $G$

Theory: IS $\leq_p$ Clique

• Can be proved using the same method by reversing the function

Theory: $VC\leq_p IS$, $IS\leq_p VC$

Lemma: In graph $G=<V, E>$, $S\leq V$ is a $VC$ iff $V\setminus S$ is an $IS$

Proof: (<=)

If $V\setminus S$ is $IS$, then any edge $(u, v)$ can't have both $u, v$ in $V\setminus S$. That is, at least one of $u, v$ in $S$

Thus, $S$ is $VC$

(=>)

If $S$ is $VC$, for any $(u, v)\in E$, one of $u, v$ is in $S$. That is, we can't have both $u, v$ in $V\setminus S$. Therefore, $V\setminus S$ is $IS$

$VC \leftrightarrow IS$

$<G, k>\leftrightarrow <G, n-k>$

HP: path

HC: cycle

Theorem: $HP\leq_p HC$

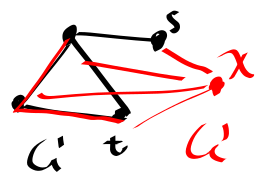
$G$ has HP $\Leftrightarrow$ $G'$ has a HC

Theorem: $HC\leq_p HP$