More Reductions

Hamiltonian Cycle to Travelling Salesman

$HC\leq_p TSP$

• Edges have weights in TSP
• Minimize weight in a cycle

• Is there a cycle with total weight $\leq k$ $(G', k)$

$<G', n>$, where $n=G$

We can prove

$G$ is yes $\Rightarrow$ $<G', n>$ is yes

Also need to prove

$no\Rightarrow no$

$yes \Leftarrow yes$ - easier to prove

NP

P - polynomial time

NP - non-deterministic polynomial time

Clique: $<G, k>$

Matching: $<G, k>$

$|v'|=k,\forall u, v \in V', (u, v)\in E$

Note: solution and proof are different

• For the above two problems, it happens that the proof = solution

Definition of NP

A decision problem $X$ is in NP if an only if $\exists$ a polynomial time algorithm $V$ such that

• An instance is "yes" instance $\exists$ a polynomial length string $y$ s.t. $V(x, y)=yes$
• An instance $x$ is "no" instance $\Rightarrow$ no $y$ can make $V(x, y)=yes$

Consider the Clique problem again

$Clique\in NP$

Vertex cover $\in NP$

$<G, k>$

$V'\in V, |V'|=k$

Bipartite graph $\in NP$

$V_\ell\cup V_r=V$

Proves

$P\subset NP$

using zero length proof

NP-Complete

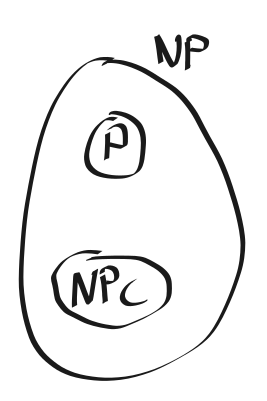
Definiton:

A problem $X\in NP$ is called NP-Complete if for every $Y\in NP$, $Y\leq_p X$

Corollary: If both $X, Y$ are $NPC$, then $X\leq_p Y$, $Y\leq_p X$

Corollary: If $X\in NPC$, and $X$ has a polynomial time algorithm, then $NP=P$

Corollary: Let $X\in NPC$, $Y\in NP$, then $X\leq_p Y$ implies $Y\in NPC$

3 SAT Problem (3 Satifiability)

CNF: Conjunctive normal form

$(x_1\vee x_2\vee\overline{x_3})\wedge(\overline{x_2}\vee\overline{x_3})\wedge(\overline{x_1}\vee x_2\vee x_3)\wedge(x_1\vee x_3)$

$x_1$ is a literal

$(x_1 \vee x_3)$ is a clause

$x_1=T, x_2=F, x_3=T$

Theory: (Cook-Levin) 3 SAT is NP-Complete

$EXACT-3SAT\leq_p 3SAT$

$3SAT\leq_p EXACT-3SAT$

$u\vee v \rightarrow \begin{cases} u\vee v \vee y\\ u\vee v \vee \overline{y} \end{cases}$

Create new variable $y$

Theory: 3SAT $\leq_p$ Independent Set
Ideas: variable $T \rightarrow$ vertex is selecte

$(\overline{x}\vee y\vee \overline{z}),(x\vee\overline{y}\vee z), (x, \vee y\vee z), (\overline{x}\vee \overline{y})$

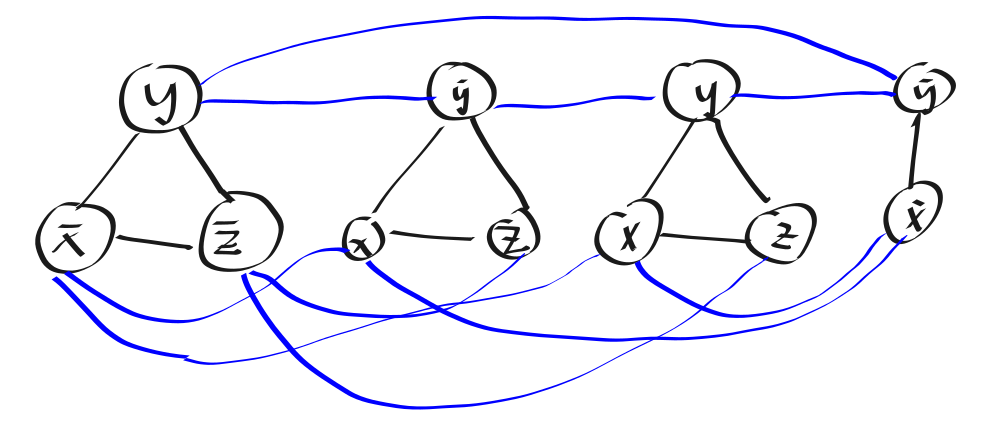
1. Polynomial time $v$
2. $yes \Rightarrow yes$
   1. If satisfiable, then there are truth assignments to the variables s.t. each caluse has at least 1 true literal
3. $yes\Leftarrow yes$

Corollary: Independent Set $\in NPC$

To prove this

1. $IS\leftarrow NP$
2. $3SAT\leq_p IS$

$3SAT\leq_p IS \leq_p VC$

$3SAT\leq_p IS\leq_p Clique$