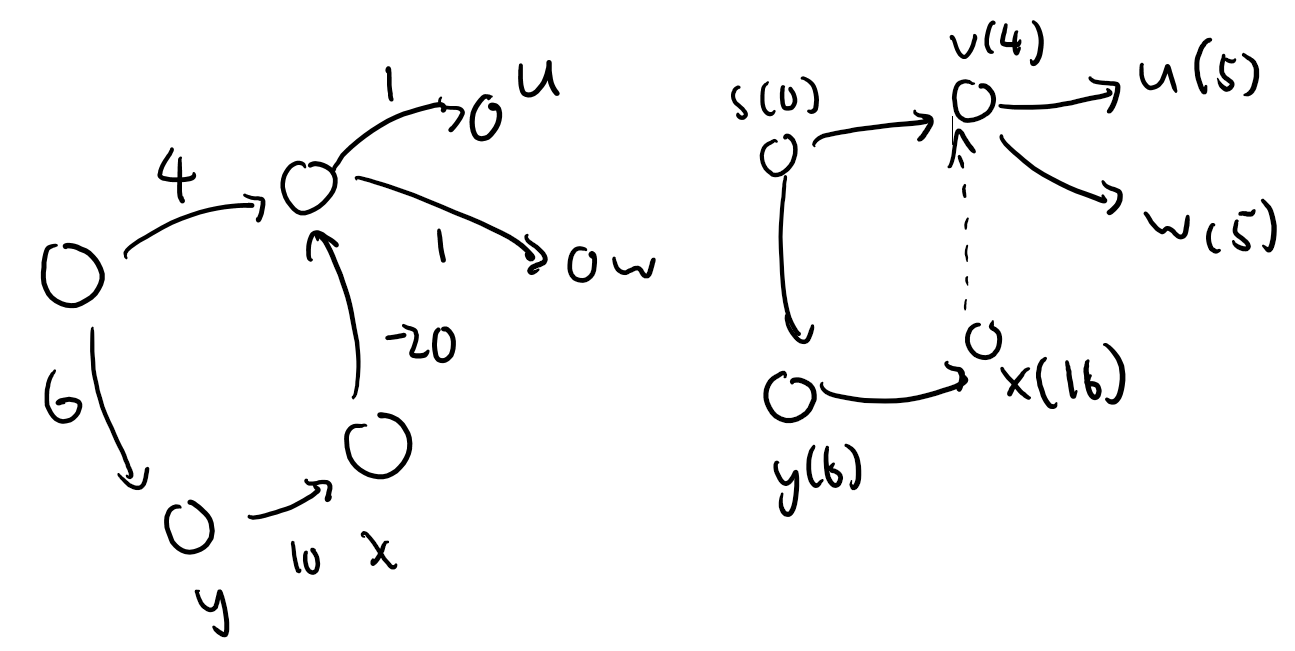
Compute Shortest Path
If v∈T
d[v] = shortest path length from s to v on the tree T
If v∉T
d[v]=min{u∈T & (u,v)∈E}(d[u]+w(u,v))
d[v]=∞ if no (u,v)∈E for any u←T
- Let T contains only s
- d[s]←D and d[v]←w(s,v)
- While T does not cover all vertices
- FInd v∉T that minimize x=y. Assume (u,v) is the edge that minimize d[v]
- T→T∪{(u,v)}
- For each neighbour x of v, d[x]←min{d[x],d[v]+w(v,x)}
Improved version (using priority queue)
- Delete-min: O(logn)
- Decrease-key: O(logn)
Therefore, the overall complexity is
O(n⋅logn+m⋅logn)=O((n+m)⋅logn)
The priority queue implementation is also called Dijkstra's Algorithm
Bellman-Ford Algorithm
D[v,k]:= shortest path weight that uses at most k edges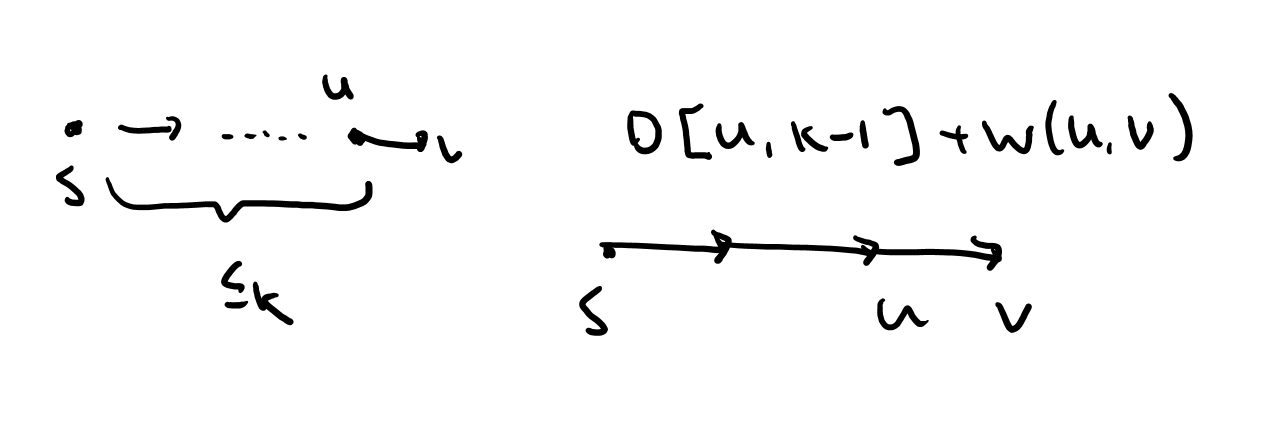
basecase{D[v,0]=∞D[s,0]=0
D[v,k]=min(u,v)∈E(D[u,k−1]+w(u,v))
D[s,0]=0,D[v,0]=∞ for s≠v
D[s, 0] = 0
D[v, 0] = infinity for s != v
for k = 1 to n - 1
for v in V
D[v, k] = min{(u, v) in E} (D[u, k-1] + w(u, v))
D[*, n-1] contains the answers
Complexity
Time: O(n⋅m)
Space: O(n2)
Alternative Implementation (Better space efficiency)
d[v], p[v]
d[s] <- 0, d[v] <- infinity
p[v] <- null
for k = 1 to n - 1
for each edge (u, v) in E
if d[u]+w(u, v) < d[v]
d[v]=d[u]+w(u,v)
p[v]=u
shortestdist <= d[v] <=

