Input Performance

Input Performance Models

• Create a model of how people use input devices and interfaces to predict time, error, fatigue, learning etc.
  • The goal is to be able to evaluate different designs before building them

Keystroke Level Model (KLM)

• Describe each task with a sequence of operators
• Sum up times to estimate how long the task takes

Operator types

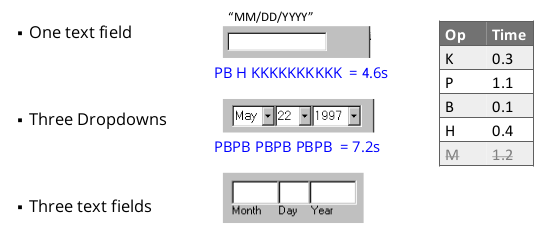
K - Keystroke = 0.08 - 1.2s

P - Pointing = 1.10s

B - Button press on mouse = 0.1s

H - Hand move from mouse to/from keyboard = 0.4s

M - Mental preparation = 1.2s

• KLM is simplified GOMS, so sometimes called KLM-GOMS
• Can be used to compare the performance time of different UI components

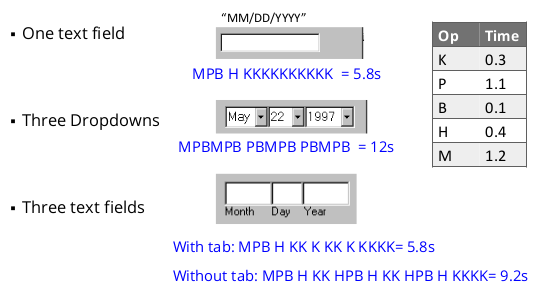
KML with Mental Operators (M)

• People need to think about something before doing it
  • Identify when people have to stop and think M
  • Difference between actions using cognitive conscious and cognitive unconscious
• Insert M when people have to
  • Initiate task
  • Make a strategy decision
  • Retrieve a chunk from memory
  • Find something on the display
  • Think of a task parameter
  • Verify that a specification/action is correct
• Add M in front of any action if the user is novice (vs. expert)

Drawbacks

• Sometime estimates are out of date
• Some time estimates are inherently variable
• Doesn't model errors, learning time etc.
• Doesn't model pointing very well
  • Some device are faster than the others

Fitts' Law

• Published in 1954
• A predictive model for priting time considering device, distance and target size
• Based on rapid, aimed movements
• Works for many kinds of pointing devices
  • Finger, pen, mouse, joystick etc.

• By Paul Fitts

  • Psychologist at Ohio State University
  • Early advocate of user-centered design

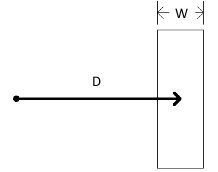
• Larger distance => longer time

• Smaller sized target => longer time

$MT\propto \frac{D}{S}$

$MT=a+b\log_2 (\frac{D}{W}+1)$

• This is Fitts' law

MT - movement time

D - distance between the starting point of the center of the target

W - constraining size of the target

a, b - characterstics of the input device

IP (Index of Performance)

Can be characterized by $1/b$

ID (Index of difficulty)

$\log_2 (\frac{D}{W}+1)$

For 2D targets

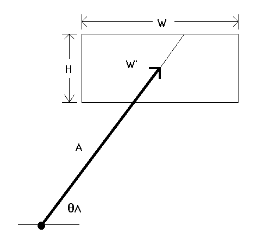
• To determine the "W" in Fitts' Law, we take the minimum of W and H

$MT=a+b\log_2(\frac{D}{\min(W, H)}+1)$

Context vs. Pie Menus

• Context menu lowers D, but some items are closer than others
• Pie menus give all items same D

Motor Space vs. Screen Space

• Dynamically change CD Gain based on position of cursor

  • Make the cursor move slowly when over the button
  • This makes the button larger in motor space while remaining the same in screen space

• The OSX dock expands in visual space but not motor space

  • Selecting an item on the expanded dock is no easier than the default dock according to Fitts' law

Steering Law

• An adaptation of Fitts' Law
• Developed by Zhai and Acott

• Choose a paradigm which focuses on steering between boundaries

• Subjects passed a stylus from one end to the other

  • As fast as possible
  • Between each goal
  • Several trials with different amplitudes (A) and widths (W)
• Same law as Fitts' tapping task

Only one goal

$ID_1=\log_2(\frac{A}{W}+1)$

With N goals

$ID_N=\log_2(\frac{A}{N\times W}+1)$